| Issue |
RAIRO-Theor. Inf. Appl.
Volume 34, Number 3, May/June 2000
|
|
|---|---|---|
| Page(s) | 173 - 181 | |
| DOI | https://doi.org/10.1051/ita:2000113 | |
| Published online | 15 April 2002 | |
Approximation Algorithms for the Traveling Salesman Problem with Range Condition
1
Lehrstuhl für Informatik I, RWTH Aachen, 52056 Aachen, Germany
2
Department of Computer-Science, Indian Institute of Technology, Madras 600036, India
3
Department of Computer-Science, Indian Institute of Technology, Madras 600036, India; (rangan@iitm.ernet.in)
Received:
12
January
2000
Accepted:
13
February
2000
We prove that the Christofides algorithm gives a 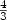 approximation ratio for the
special case of traveling salesman problem (TSP) in which the maximum weight in the given
graph is at most twice the minimum weight for the odd degree restricted graphs. A
graph is odd degree restricted if the number of odd degree vertices in any minimum
spanning tree of the given graph is less than
approximation ratio for the
special case of traveling salesman problem (TSP) in which the maximum weight in the given
graph is at most twice the minimum weight for the odd degree restricted graphs. A
graph is odd degree restricted if the number of odd degree vertices in any minimum
spanning tree of the given graph is less than  times the number of vertices
in the graph. We prove that the Christofides algorithm is more efficient
(in terms of runtime) than the previous existing algorithms for this special case of the
traveling salesman problem. Secondly, we apply the concept of stability of approximation
to this special case of traveling salesman problem in order to partition the set of all
instances of TSP into an infinite spectrum of classes according to their approximability.
times the number of vertices
in the graph. We prove that the Christofides algorithm is more efficient
(in terms of runtime) than the previous existing algorithms for this special case of the
traveling salesman problem. Secondly, we apply the concept of stability of approximation
to this special case of traveling salesman problem in order to partition the set of all
instances of TSP into an infinite spectrum of classes according to their approximability.
Mathematics Subject Classification: 68W25 / 05C85 / 68W40
© EDP Sciences, 2000
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


