| Issue |
RAIRO-Theor. Inf. Appl.
Volume 35, Number 4, July/August 2001
|
|
|---|---|---|
| Page(s) | 379 - 388 | |
| DOI | https://doi.org/10.1051/ita:2001125 | |
| Published online | 15 April 2002 | |
On the expressive power of the shuffle operator matched with intersection by regular sets
1
Institute of Mathematics, University of Gdańsk,
ul Wita Stwosza 57, 80952 Gdańsk, Poland; (jj@math.univ.gda.pl)
2
Institute of Mathematics, University of
Gdańsk,
ul Wita Stwosza 57, 80952 Gdańsk, Poland; (matszp@math.univ.gda.pl)
Received:
December
2000
Accepted:
October
2001
We investigate the complexity of languages described by some expressions
containing shuffle operator and intersection. We show that deciding whether
the shuffle of two words has a nonempty intersection with a regular set
(or fulfills some regular pattern) is NL-complete.
Furthermore we show that the class of languages of the form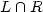 
,
with a shuffle language L and a regular language R, contains
non-semilinear languages and does not form a family of mildly
context- sensitive languages.
Mathematics Subject Classification: 68Q15 / 68Q45
Key words: Formal languages / shuffle / space complexity.
© EDP Sciences, 2001
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.