| Issue |
RAIRO-Theor. Inf. Appl.
Volume 33, Number 2, March April 1999
|
|
|---|---|---|
| Page(s) | 159 - 176 | |
| DOI | https://doi.org/10.1051/ita:1999100 | |
| Published online | 15 August 2002 | |
Immunity and Simplicity for Exact Counting and Other Counting Classes
Institut für Informatik,
Friedrich-Schiller-Universität Jena,
07740 Jena, Germany; rothe@informatik.uni-jena.de.
Received:
January
1998
Accepted:
March
1999
Ko [26] and Bruschi [11] independently showed that, in
some relativized world, PSPACE (in fact, ⊕P) contains a set
that is immune to the polynomial hierarchy (PH). In this paper, we
study and settle the question of relativized separations with
immunity for PH and the counting classes PP,  , and ⊕P
in all possible pairwise combinations. Our main result is that there
is an oracle A relative to which
, and ⊕P
in all possible pairwise combinations. Our main result is that there
is an oracle A relative to which  contains a set that is immune BPP⊕P.
In particular, this
contains a set that is immune BPP⊕P.
In particular, this  set is immune to PHA and to ⊕PA. Strengthening results of
Torán [48] and Green [18], we also show that, in suitable relativizations,
NP contains a
set is immune to PHA and to ⊕PA. Strengthening results of
Torán [48] and Green [18], we also show that, in suitable relativizations,
NP contains a  -immune set, and ⊕P contains a PPPH-immune
set. This implies the existence of a
-immune set, and ⊕P contains a PPPH-immune
set. This implies the existence of a 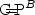 -simple set for some
oracle B, which extends results of Balcázar et al. [2,4].
Our proof technique requires a circuit lower bound for “exact
counting” that is derived from Razborov's [35] circuit
lower bound for majority.
-simple set for some
oracle B, which extends results of Balcázar et al. [2,4].
Our proof technique requires a circuit lower bound for “exact
counting” that is derived from Razborov's [35] circuit
lower bound for majority.
Mathematics Subject Classification: 68Q15 / 68Q10 / 03D15
Key words: Computational complexity / immunity / counting classes / relativized computation / circuit lower bounds.
© EDP Sciences, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


