| Issue |
RAIRO-Theor. Inf. Appl.
Volume 43, Number 2, April-June 2009
|
|
|---|---|---|
| Page(s) | 189 - 207 | |
| DOI | https://doi.org/10.1051/ita:2008024 | |
| Published online | 05 June 2008 | |
On the power of randomization for job shop scheduling with k-units length tasks
Department of Informatics,
ETH Zurich, ETH Zentrum, 8092 Zürich, Switzerland; tobias.moemke@inf.ethz.ch
Received:
28
August
2007
Accepted:
24
April
2008
In the job shop scheduling problem k-units-Jm, there are
m machines and each machine has an integer processing time of at most
k time units. Each job consists of a permutation of m
tasks corresponding to all machines and thus all jobs have an identical
dilation D.
The contribution of this paper are the
following results;
(i) for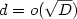 
jobs and every fixed k, the makespan of
an optimal schedule is at most D+ o(D), which extends the result of [3]
for k=1;
(ii) a randomized on-line approximation algorithm for k-units-Jm is
presented. This is the on-line algorithm with the best known competitive
ratio against an oblivious adversary for 
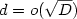and k > 1;
(iii) different processing times yield harder instances than identical
processing times. There is no 5/3 competitive deterministic on-line
algorithm for k-units-Jm, whereas the competitive ratio of the randomized
on-line algorithm of (ii) still tends to 1 for .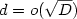
Mathematics Subject Classification: 68W20 / 68W25
Key words: On-line algorithms / randomization / competitive ratio / scheduling
© EDP Sciences, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.