| Issue |
RAIRO-Theor. Inf. Appl.
Volume 37, Number 2, April/June 2003
|
|
|---|---|---|
| Page(s) | 115 - 126 | |
| DOI | https://doi.org/10.1051/ita:2003013 | |
| Published online | 15 November 2003 | |
Undecidability of Topological and Arithmetical Properties of Infinitary Rational Relations
Équipe de Logique Mathématique,
U.F.R. de Mathématiques, Université Paris-7, 2 place Jussieu, 75251
Paris Cedex 05, France;
finkel@logique.jussieu.fr.
Received:
February
2002
Accepted:
March
2003
We prove that for every countable ordinal α one cannot decide
whether a given infinitary rational relation is in the Borel class
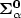(respectively 
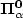). Furthermore
one cannot
decide whether a given infinitary rational relation is a Borel set or a
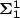-complete set. We prove some recursive analogues to these
properties. In
particular one cannot decide whether an infinitary rational relation is an
arithmetical set.
We then deduce from the proof of
these results some other ones, like: one cannot decide whether the
complement of
an infinitary rational relation is also an infinitary rational relation.
Mathematics Subject Classification: 68Q45 / 03D05 / 03D55 / 03E15
Key words: Infinitary rational relations / topological properties / Borel and analytic sets / arithmetical properties / decision problems.
© EDP Sciences, 2003
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.